Definition of Paths

Let \(G\) be a graph with vertices \(v_1\) and \(v_2.\) A path in \(G\) from \(v_1\) to \(v_2\) is a sequence of edges \(((v_1, p_1), (p_1, p_2), (p_2, p_3), \dots, (p_k, v_2))\) in \(G.\)

---

Zero or more paths may exist for any two vertices \(v_1\) and \(v_2.\)

A simple path is a path in which no vertex is repeated.

Example

Let \(G\) be an undirected graph with vertex set \(V = \{1,2,3,4,5,6\}\) and edge set \(\{(1,2), (1,3), (2,4), (3,5), (4,5), (4,6)\}\) with their corresponding pairs. A path from \(1\) to \(6\) would be \((1,2,4,6).\) That is, first go from \(1\) to \(2,\) then \(2\) to \(4,\) then \(4\) to \(6.\) Here is a picture of the path with the path drawn in red arrows: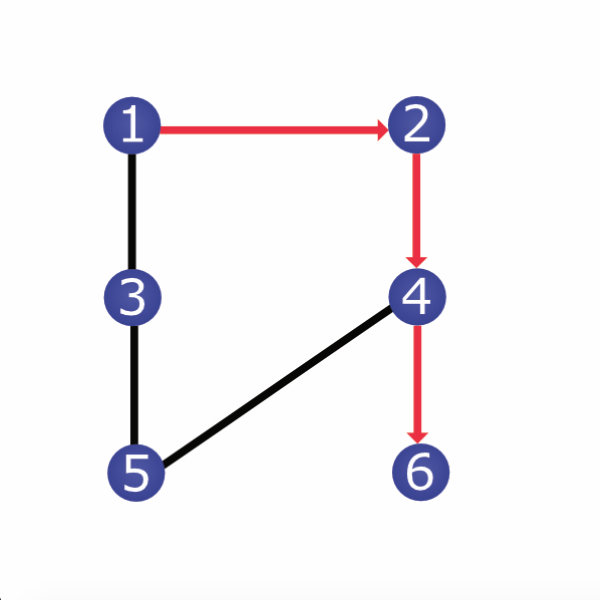

Since the path does not visit any vertex more than once, it is a simple path.